Función sobreyectiva

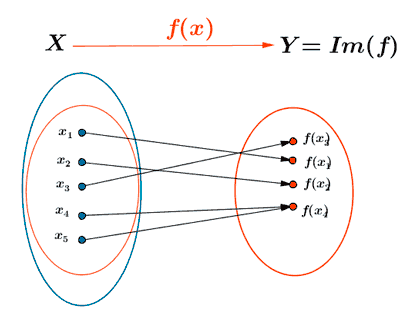
Ejemplo de función sobreyectiva.

En matemática, una función es sobreyectiva (epiyectiva, suprayectiva,¹ suryectiva, exhaustiva¹ o subyectiva) si está aplicada sobre todo el condominio, es decir, cuando cada elemento de "Y" es la imagen de como mínimo un elemento de "X".

Formalmente,

Cardinalidad y sobreyectividad

Dados dos conjuntos y , entre los cuales existe una función sobreyectiva , se tiene que los cardinales que cumplen:
Si además existe otra aplicación sobreyectiva , entonces puede probarse que existe una aplicación biyectiva entre A y B.

Sobreyectivo (o también "epiyectivo")

Una función f (de un conjunto A a otro B) es sobreyectiva si para cada y en B, existe por lo menos un x en A que cumple f(x) = y, en otras palabras f es sobreyectiva si y sólo si f(A) = B.
Así que cada elemento de la imagen corresponde con un elemento del dominio por lo menos.

Ejemplo: la función f(x) = 2x del conjunto de los números naturales al de los números pares no negativos es sobreyectiva.
Sin embargo, f(x) = 2x del conjunto de los números naturales a no es sobreyectiva, porque, por ejemplo, ningún elemento de va al 3 por esta función.

Función sobreyectiva

Una función  f: X → Y  es una función sobreyectiva si:
Im(f) =Y
Esto significa que todo elemento  y ∈ Y  es la imagen de al menos un elemento  x ∈ A . Es decir, la imagen de  f  coincide con el conjunto final.

Ejemplo de función sobreyectiva

a)   Veamos si la función  f: R → R , donde  f(x) = x² + 1, es sobreyectiva:

En este caso:

            El conjunto inicial de f es R .
            El conjunto final de f es:    R
           La imagen de f es [1 , ∞), es decir:    Im(f) = [1 , ∞)
            La imagen de f y el conjunto final de f no coinciden:

            Vease la parte rayada del eje OY. No coincide con todo R
Luego la función f no es sobreyectiva.

                

b)   Veamos si la función  g: R → R , donde  g(x) = x³ + 3, es sobreyectiva:

En este caso:

            El conjunto inicial de g es R .
            El conjunto final de g es:    R
            La imagen de g es también R , es decir:    Im(g) = R
            La imagen de g y el conjunto final de g coinciden es    R:

            Vease la parte rayada del eje OY. Coincide con todo R

Luego la función g sí es sobreyectiva.